大学の課題で生み出してしまった謎グラフ、解明してみた

こんにちは。今年新卒で入社しました、コザキです。

初のテックブログ執筆ということで、何を書くか悩んだのですが、学生時代に生み出してしまった変なグラフを紐解き、なぜそんな異物が生成されてしまったのかを考えてみたいと思います。
正しい結果を出力するコードに修正することを目的として進めます。バグではありませんが、ある種のデバッグです。
なお、p5.jsを利用しています。

目的のアニメーション

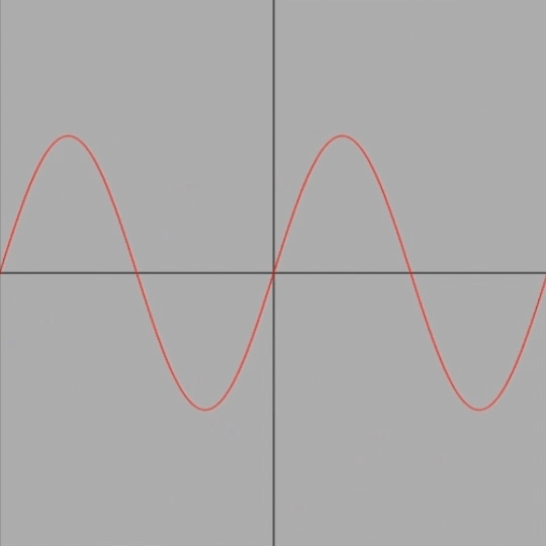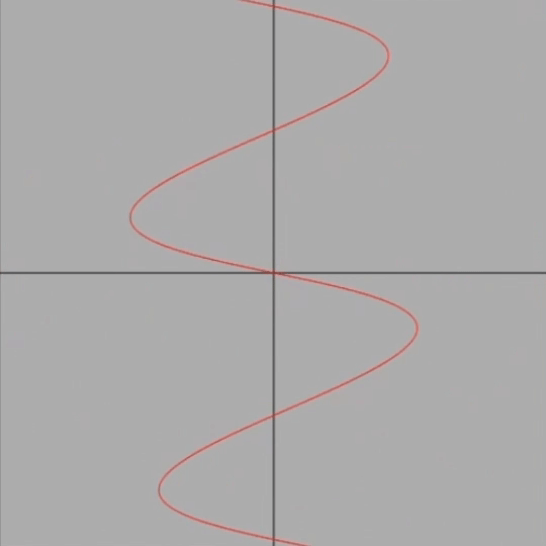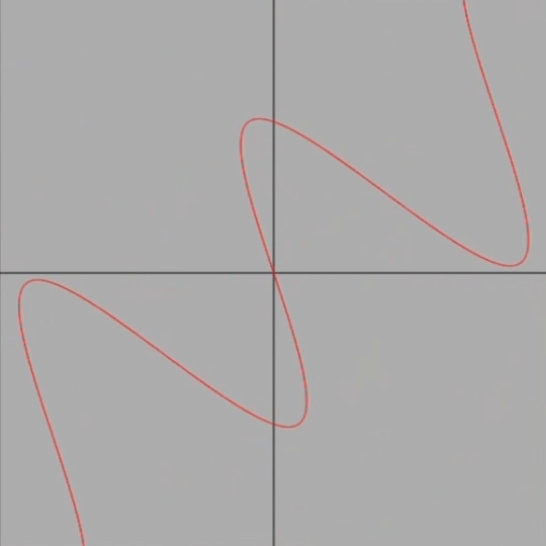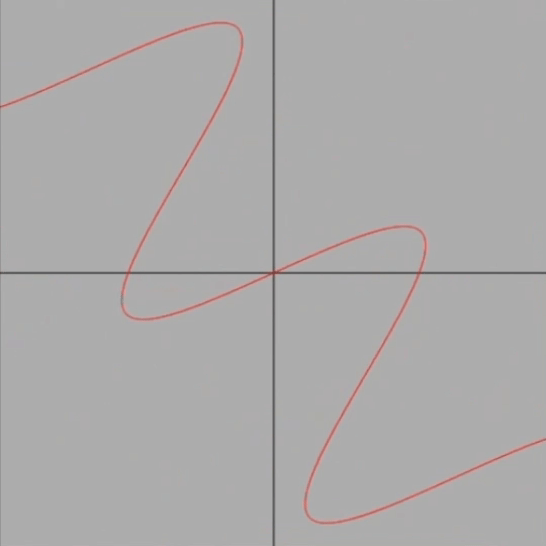
簡単に言えば、y=sin x（以後sin xと表記）のグラフを、反時計回りで原点中心にくるくる回すアニメーションです。

実際に生成されたアニメーション

どうしてこうなった？？？

明らかに線が多いですね。それに、1本1本の線がsin xのような波形のグラフになっていないように見えます。
あまりにもごちゃごちゃしているので、これを見るだけで問題点をすべて洗い出すのは至難の業でしょう。
ここは、このアニメーションを生成したコードを読んで、何が間違っているのかを考えてみることにします。

コードを読む

目的のアニメーションを描画するためにどのようにコードを書くか、方針を先に決めておきましょう。
今回はsin xのグラフを回転させるアニメーションを描画するので、おおまかに

1. sin xのグラフを描画するコードを書く
2. 1のコードを、グラフの角度を少しずつ変えてループさせるコードを書く（1も回転に対応できるように書く）

といった形になるかと思います。これを踏まえて、実際の失敗のコードを見てみましょう。

以下のコードが、この不思議なグラフを生み出した元凶です。順に読み解いてみましょう。（HTMLファイルは割愛）

var ox, oy;
var x, y;
var xscale, yscale;
 
function setup() {
    createCanvas(500, 500);
    frameRate(15);
    ox = width/2;
    oy = height/2;
    xscale = ox/(2*PI);
    yscale = oy/2;
    t = 0;
}
 
function draw() {
    background(175);
    stroke(0);
    line(0, oy, width, oy);
    line(ox, 0, ox, height);
    stroke(255, 0, 0);
    x1 = x;
    y1 = y;
    for(x = -2*PI; x <= 2*PI; x += 0.01) {
        y = sin(x);
        x1 = x*xscale*cos(t*2*PI/15)-y*yscale*sin(t*2*PI/15)+ox;
        y1 = x*xscale*sin(t*2*PI/15)+y*yscale*cos(t*2*PI/15)+oy;
        x2 = x*xscale*cos(t*2*PI/15)+y*yscale*sin(t*2*PI/15)+ox;
        y2 = -x*xscale*sin(t*2*PI/15)+y*yscale*cos(t*2*PI/15)+ox;
        line(x1, y1, x2, y2);
        t++;
        x1 = x;
        y1 = y;
    }
}

ひとまず間違いの指摘は後に回すとして、どのような動作をさせようとしてコードを書いているのか、上から解説していきます。
皆さんも、ぜひ失敗の原因を探しながら読んでみてください。

varで定義している変数はいったん置いておいて、まずはfunction setup()を見てみます。ここでは、アニメーションを描画するための前準備を行います。
createCanvas(500, 500);で描画領域を用意しています。ここで気を付けるべきなのは、普段よく見るデカルト座標と異なり、yが大きくなるほど画面の下の方に描画されるという点です。簡単に言えば、yだけ上下が反転している、ということです。非常にややこしいですね。
次に、frameRate(15);で1秒間に描画する回数を決めています。
ox、oyは、それぞれy軸のx座標、x軸のy座標を示していますね。すなわち、座標(ox, oy)はグラフの原点です。
xscale、yscaleは、グラフの縮尺を整えるためのスケール関数です。

次にfunction draw()です。この関数は、何度も繰り返し呼び出される関数です。これが今回の方針の②のコードになります。
ここで注意しておきたいのが、方針からわかるように、1回のdrawループで何度もグラフを描画しているのではなく、draw()の中身を1回実行するごとに1つのグラフを描画する、ということです。
つまり、下記の画像のように描画するグラフの角度を1drawループ（1描写）ごとに少しずつ変えて回転しているように見せる、というアニメーションになります。

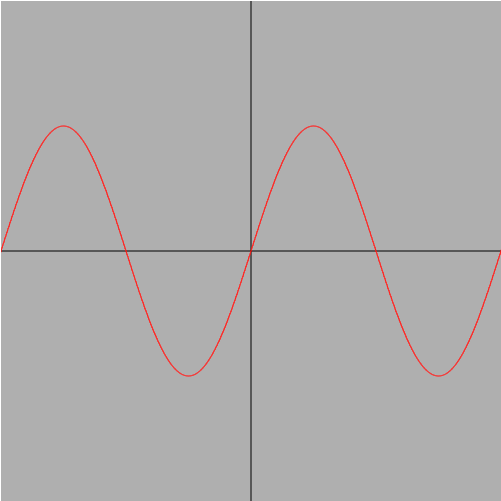
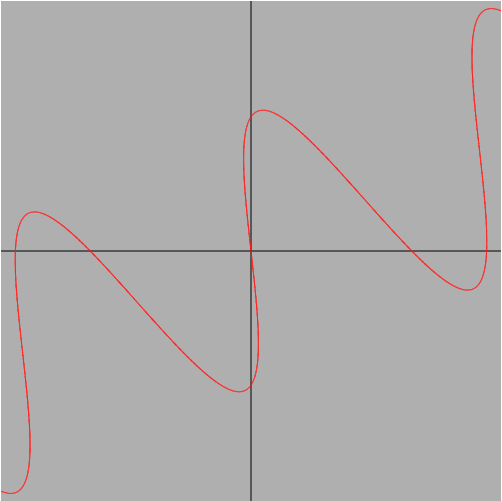
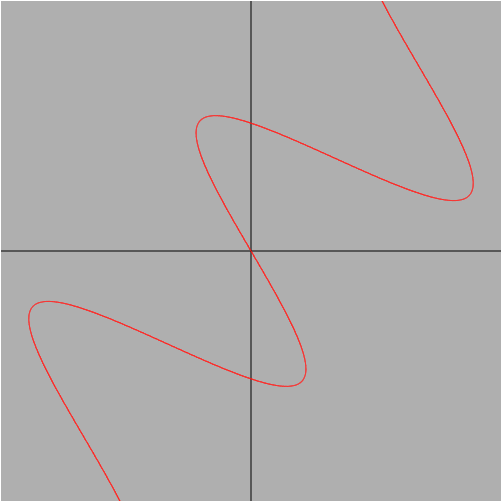
これを頭の片隅に置いておくだけでも、格段にコードを理解しやすくなるかな、と思います。

改めて中身を見てみましょう。forループでx=-2*PIからx=2*PIまで回していますが、これは回転角ではなく、回転させるsin xのグラフ自体を描画するための数値ですね。
中身を見てみると、なにやらごちゃごちゃと代入しています。これは、回転した後の座標を表す式ですね。
x1, x2, y1, y2それぞれに回転行列を掛けています。参考までに、反時計回りにθラジアン回転させる回転行列は、下記のようになります。

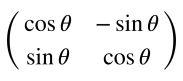
x1, x2, y1, y2は　t*2*PI/15、すなわち2πt/15。フレームレート（1秒間に描画する枚数）が15なので、1秒に1回転させようとしているようです。

次の記述を見てみましょう。

line(x1, y1, x2, y2);
t++;
x1 = x;
y1 = y;

とあります。
line(x1, y1, x2, y2);は、座標(x1, y1)と(x2, y2)をつなげて線分を描画する記述ですね。
下記の画像のように、x1 = x; y1 =y;で1forループごとに少しずつずらして描画しようとしているようです。

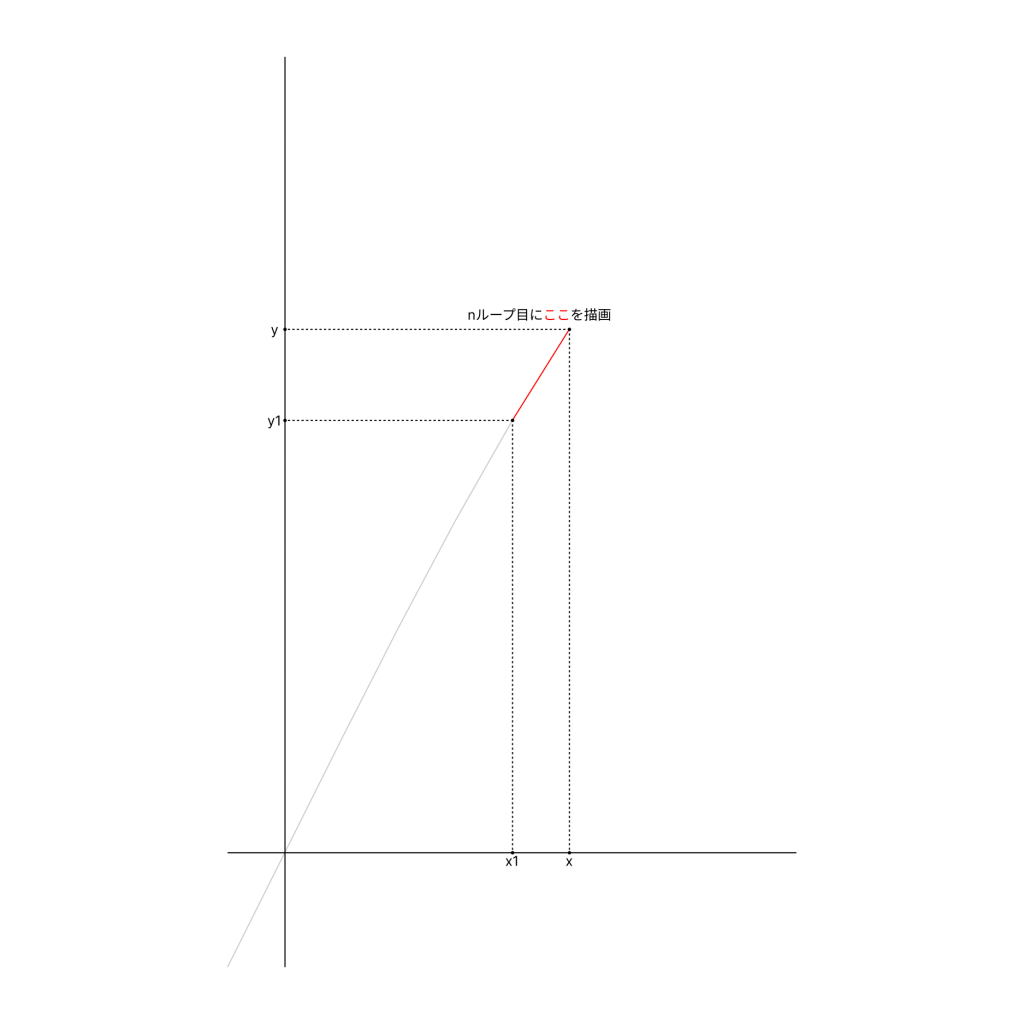
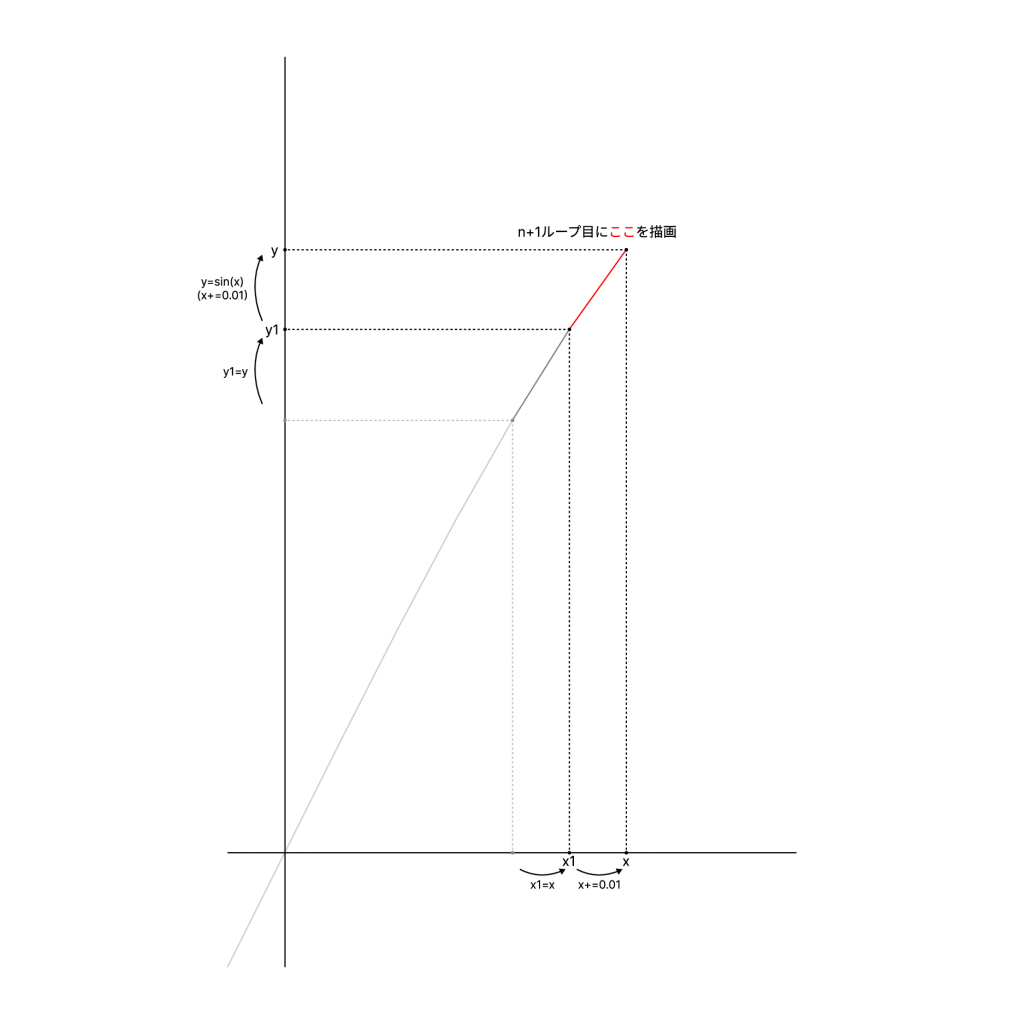
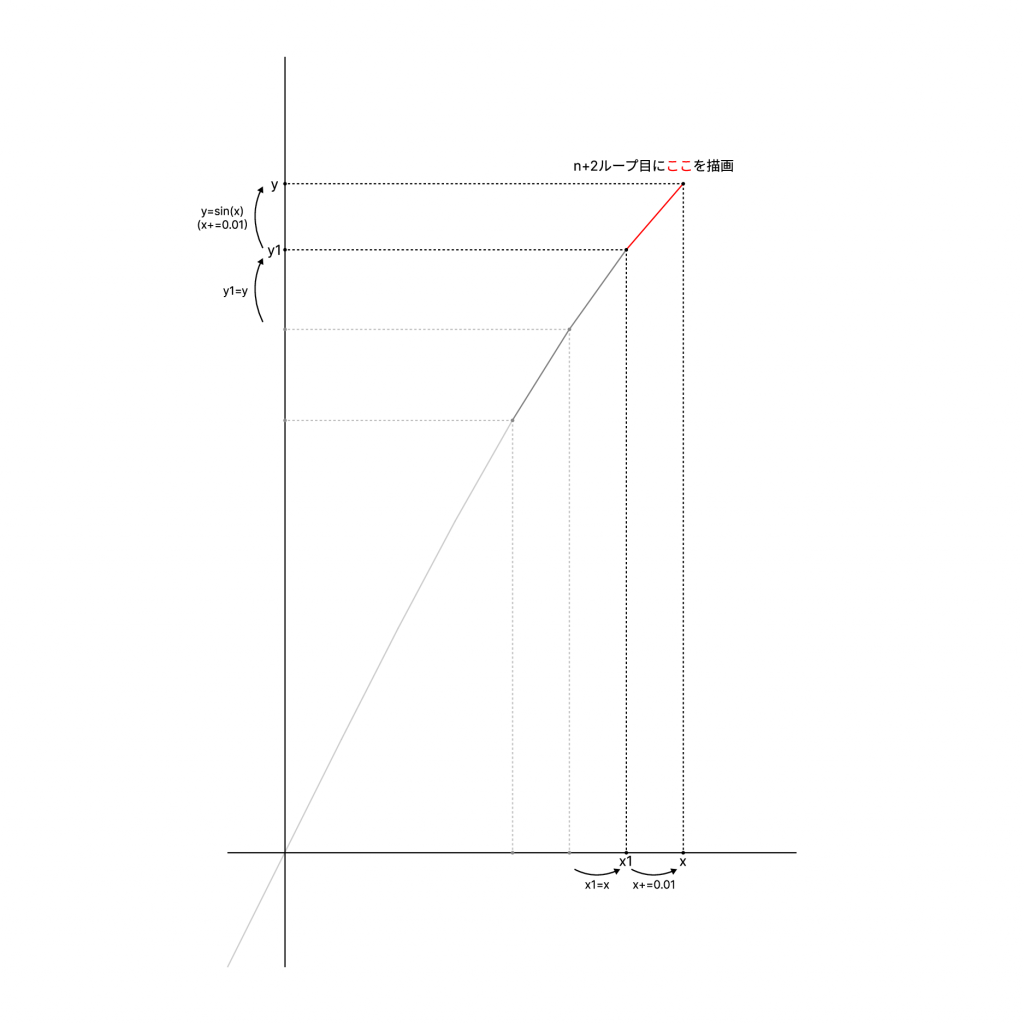
また、t++;によって、1forループごとに回転角を変えて描画するようになっています。

…さて、皆さんはどこがおかしいかわかりましたか？

修正点

今回のグラフで修正すべき点は3つ。すべてforループ内にあります。

1つ目

まず1つ目。回転行列を掛けた式の代入先です。
ここで表さなければならないのは、(x, y)、(x1, y1)をそれぞれ回転させた後の座標。しかし、最初の代入式で、回転前の座標であり基準となるはずのx1の値を変えてしまっています。そうなれば、それ以降の代入式もずれていくのは必然ですね。

したがって、代入先には別の変数を用意する必要があります。ここでは、新たにx_1, x_2, y_1, y_2を用意してやることにしましょう。

2つ目

次に2つ目。回転行列を掛けた式です。
それも、3つも間違っている点があります（修正すべき点としてはまとめて1つとカウントします）。

1点目は、x_1, y_1に代入する式に、用意したx1, y1を使っていないことです。なぜこんな式が現れたのか…。実は他の課題でsin xを描画した際は、微小な線分ではなく点をつなげる手法を用いていたのですが、それをついこちらにも流用してしまったためです。

ともあれ、せっかくなのでx1, y1を代入式に適用してあげましょう。やり方は簡単、代入式の右辺のxをx1に、yをy1に置き換える。たったこれだけです。

2点目は、x_1, y_1に代入する式とx_2, y_2に代入する式に掛けている行列が異なることです。
前者は反時計回りに回転させる回転行列を、後者は時計回りに回転させる回転行列を掛けてしまっています。
今回は反時計回りに回転させるのですから、後者にも同じ回転行列を掛ける必要がありますね。

3点目は、先述した「yだけ上下が反転している」ことを考慮できていないことです。
したがって、y_1, y_2の代入式には、「+oy」を除いて全体にマイナスを掛けなければいけません。これを怠ると、-sin xのグラフを回転させていることになってしまいます。
（ぶっちゃけて言えば、回転しているので、sin xが-sin xになっていることなんてそうそう気づかれないだろうとは思いますが…）

3つ目

最後に3つ目。t++;の位置です。
先ほど、「描画するグラフの角度を1drawループ（1描写）ごとに少しずつ変えて回転しているように見せる」と述べたと思います。しかし、今のt++;の位置では、1「for」ループごとに回転角を変えてしまっているのです。これでは、微小な線分を1forループごとに1本描画してつなげるという構造上、sin xのグラフ自体が歪んでしまいます。当然、正しく描写されるはずもありません。

では、t++;をどこに置けばいいのかというと、1drawループに1回tの値を変えればいいのですから、function draw()内の一番最後の行に移動させてやればいいわけです。

以上を元に、修正したコードが以下の通りになります。実行結果は、目的のアニメーションの通りです。

var ox,oy;
var x,y,x1,y1;
var xscale,yscale;
 
function setup(){
    createCanvas(500,500);
    frameRate(15);
    ox=width/2; oy=height/2;
    xscale=ox/(2*PI); yscale=oy/2;
    t=0;
}
 
 
function draw(){
    background(175);
    stroke(0);
    line(0,oy,width,oy);
    line(ox,0,ox,height);
    x=-3*PI;
    y=sin(x);
    stroke(255,0,0);
    x1=x;
    y1=y;
    for(x=-3*PI;x<=3*PI;x+=0.01){
        y=sin(x);
        x_1=x1*xscale*cos(t*2*PI/15)-y1*yscale*sin(t*2*PI/15)+ox;
        y_1=-(x1*xscale*sin(t*2*PI/15)+y1*yscale*cos(t*2*PI/15))+oy;
        x_2=x*xscale*cos(t*2*PI/15)-y*yscale*sin(t*2*PI/15)+ox;
        y_2=-(x*xscale*sin(t*2*PI/15)+y*yscale*cos(t*2*PI/15))+oy;
        line(x_1,y_1,x_2,y_2);
        x1=x;
        y1=y;
    }
    t++;
}

なお、for文の初期値と条件式は、そのままではグラフの描画範囲が足りなかったため、少々値をいじってあります。

振り返って

何とかグラフを正しく描画させることに成功しましたね。
見た目はとんでもない生成物でしたが、終わってみれば一つ一つはありがちなミスと言えるものばかりでした。

今回解決に至った要因は2つ。後付けとはいえ、どのように目的のものを完成させるかの方針を立てたこと。そして、その方針を元に、一つずつミスを探したことです。

先に述べたように、複雑に絡み合った要因を、一度ですべて解決することは困難を極めます。方針を立て、そこからずれている部分を探してみる。今回の例に限らず、非常に有用な考え方だと思っています。

また、目的地を明確にし、そこに至るための手順をおおまかにでも書き出してみることで、「ここに問題があるのではないか？」という仮説も立てやすくなります。

記事上では内容を理解しやすくするために一通りコードの解説をしましたが、実際の思考としては、

sin xを描画するというプロセスがあるのに、出力されたアニメーションにはsin xの面影もない
↓
sin xのグラフの描画を行っている部分に問題があるのでは
↓
この中で考えられるミスとしては、「初期値・条件値が間違っている」「代入式が間違っている」「ループ前の処理が間違っている」のどれかの可能性が高い

と仮説を立てて、そこを重点的に検証しました。これを繰り返すことでだんだん目的の形に近づき、細かい問題点も見つけやすくなります。
（つい最近知りましたが、この思考法を「アブダクション（仮説推論）」と呼ぶようです）

実際の業務では、もっと規模の大きいプログラムを扱うかと思いますが、プログラム全体の動きや目的を理解→仮説を立てて検証という思考自体は、スケールが大きくなっても活かせるはずです。
むしろ規模が大きいほど、検証範囲を絞り込めるこのやり方は活躍してくれることでしょう。

もし「隅から隅までコード読んでデバッグしてたぜ！」という方がいれば、ぜひ試していただけると嬉しいです。
皆さんのデバッグ生活に、この記事が少しでも役に立つことを願っています。